Some conference tournaments begin this weekend, and the NCAA tournament outlook for most teams is already pretty well known. Only about 15 teams (of 60) have a fair amount of uncertainty as to whether they’ll make the NCAA tournament at-large. The top 7 teams are pretty safe bets (though not all mathematical locks), leaving at most 8 slots for the 15 in question. The other 38 teams are extremely unlikely to make the NCAAs at-large, though could steal a spot from one of the 15 by winning their conference tournament.

Remember that although 16 teams make the tournament, it’s not necessarily the top 16 in PWR who make it. For each conference autobid that comes from outside the top 16, one fewer of the top 16 will get an at-large berth. Because the Atlantic Hockey autobid is sure not to be a team that would make the NCAAs at large, there are already only 15 slots available for teams to make it on the basis of their ranking. That number could be reduced if additional conference tournaments are won by teams that would not have made the tournament at-large.

Who’s (probably) in?

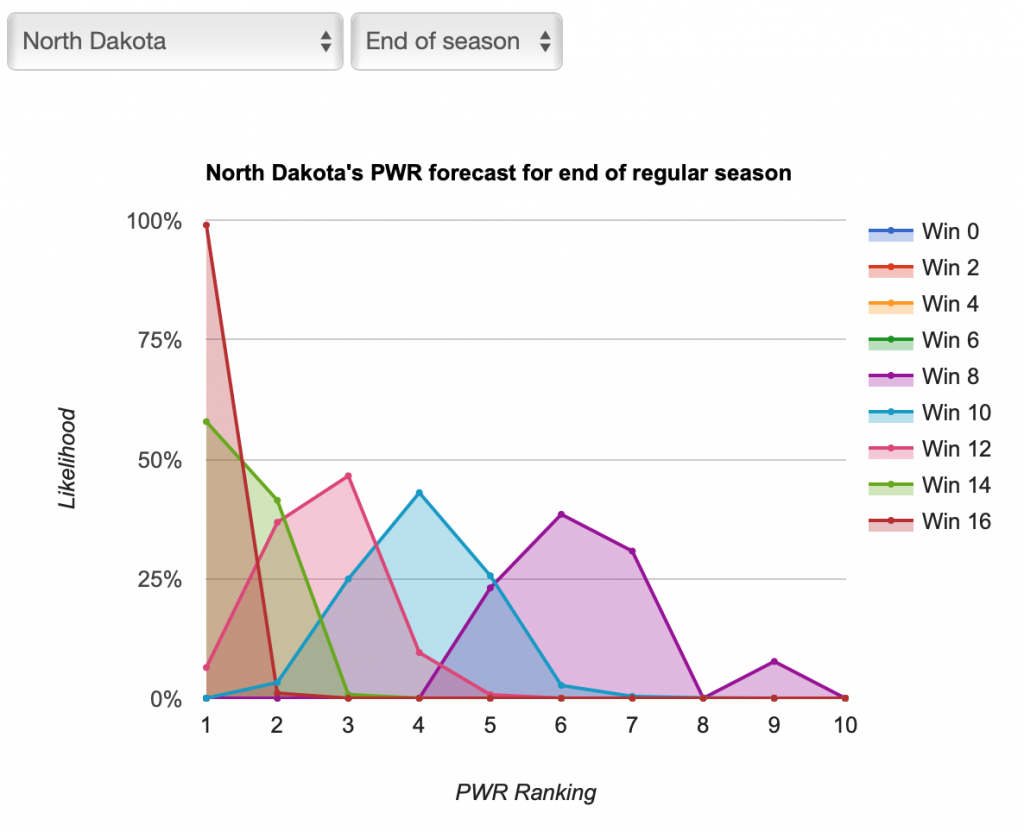
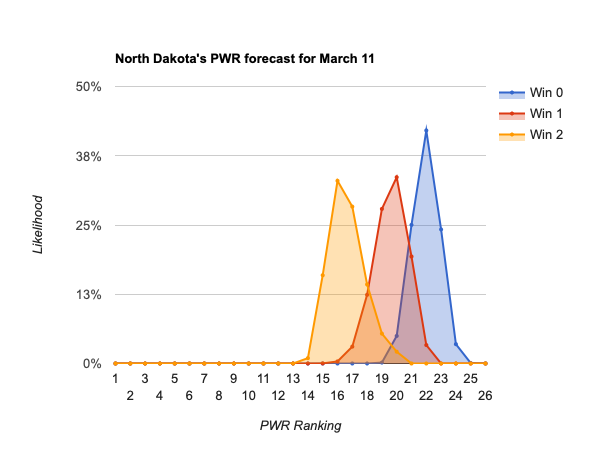
• #1 North Dakota
• #2 Minnesota St
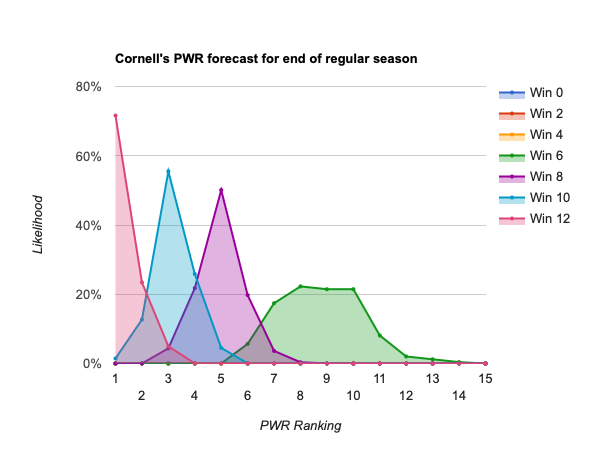
• #3 Cornell
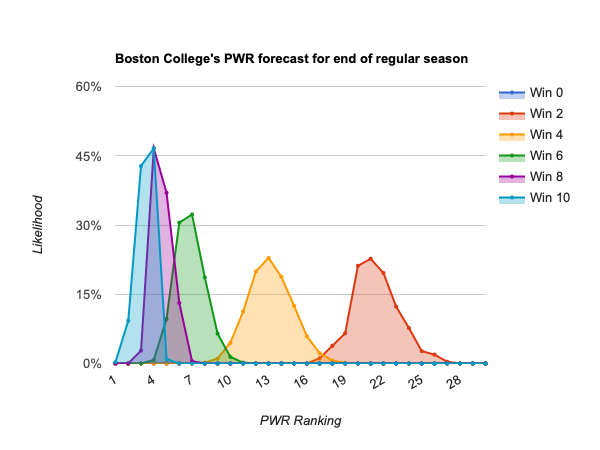
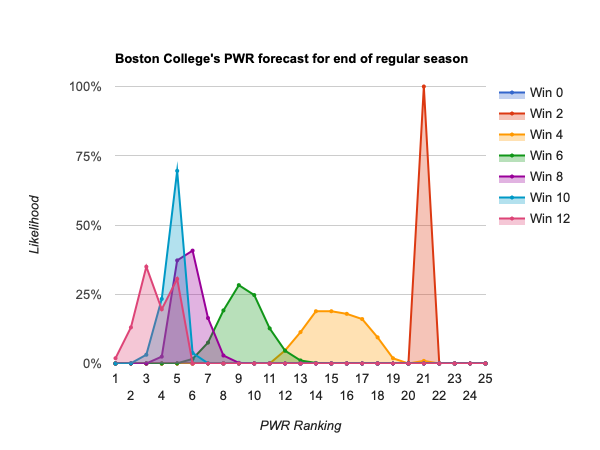
• #4 Boston College
• #5 Minnesota-Duluth
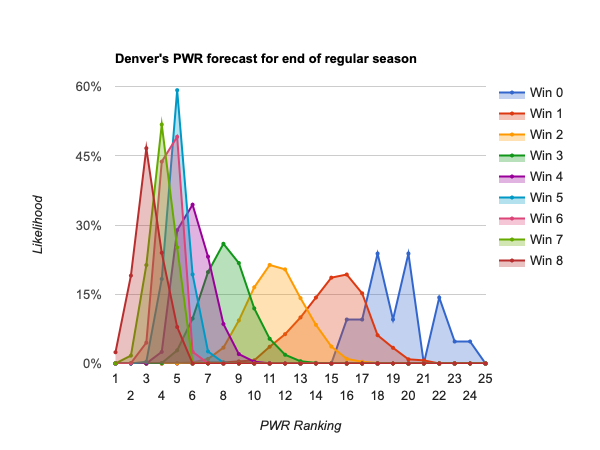
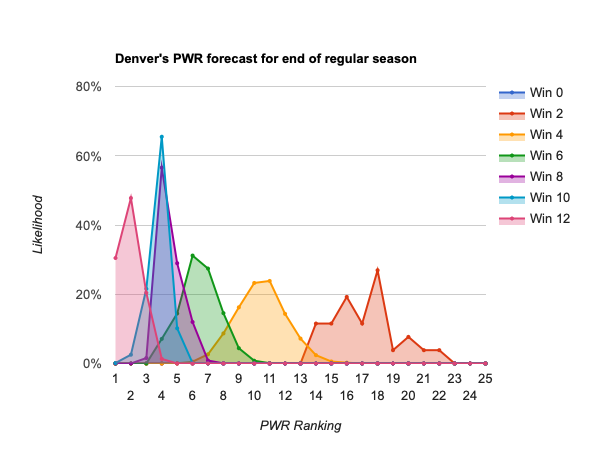
• #6 Denver
• #7 Penn St

Who’s alive no matter what happens this weekend?

• #8 Massachusetts
• #9 Clarkson
• #10 Bemidji St
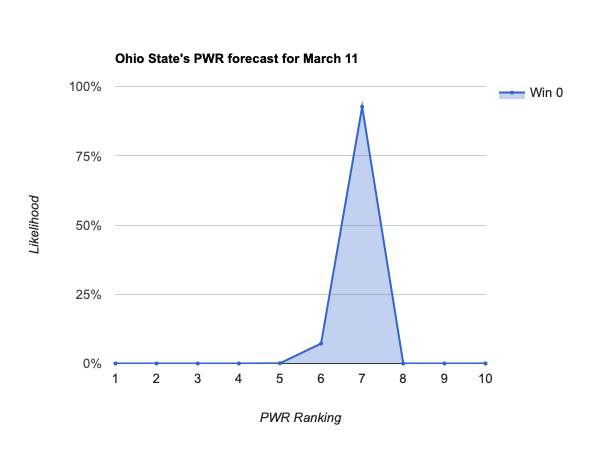
• #11 Ohio St
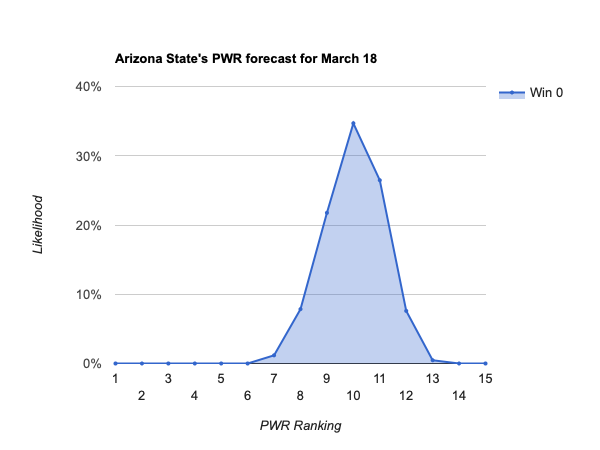
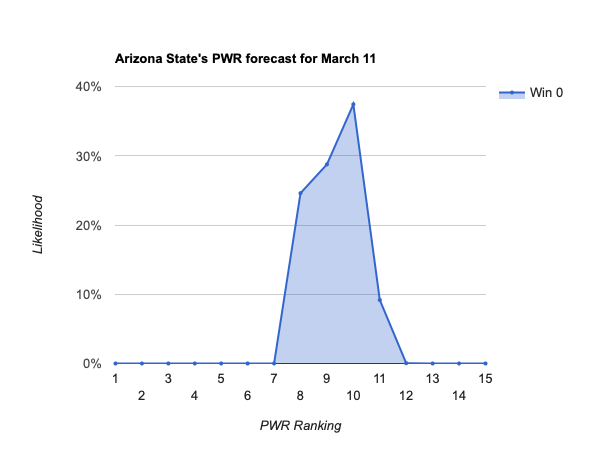
• #12 Arizona St
• #13 Mass.-Lowell
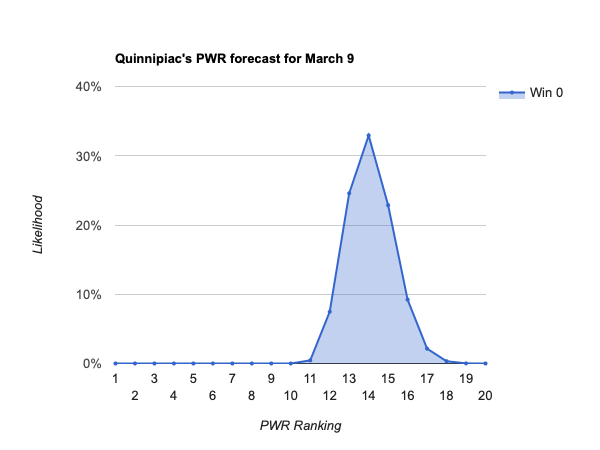
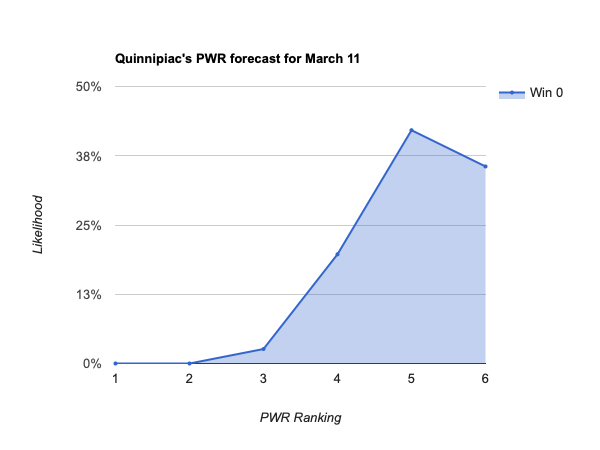
• #14 Quinnipiac

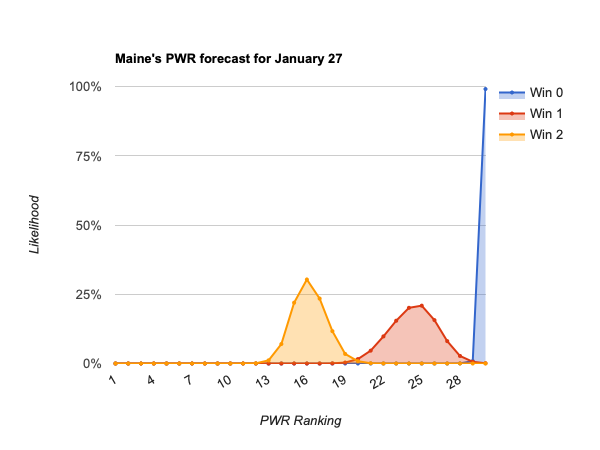
• #15 Maine
• #18 Northeastern
• #19 Western Michigan
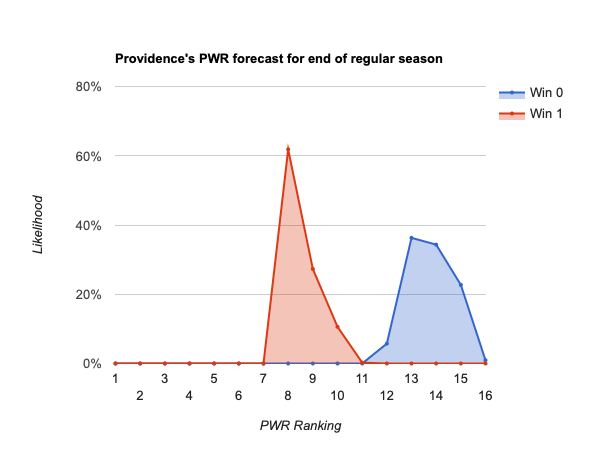
• #21 Providence
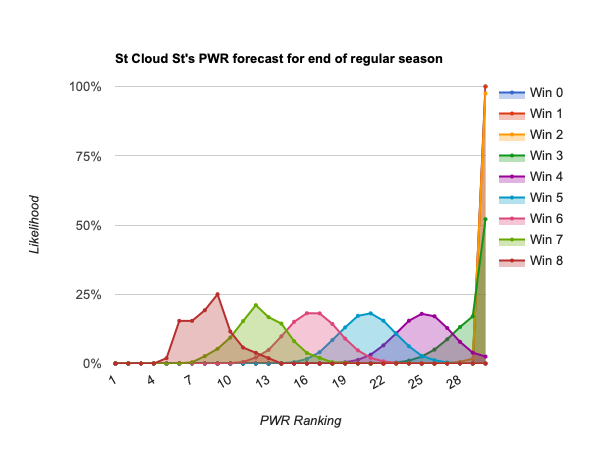
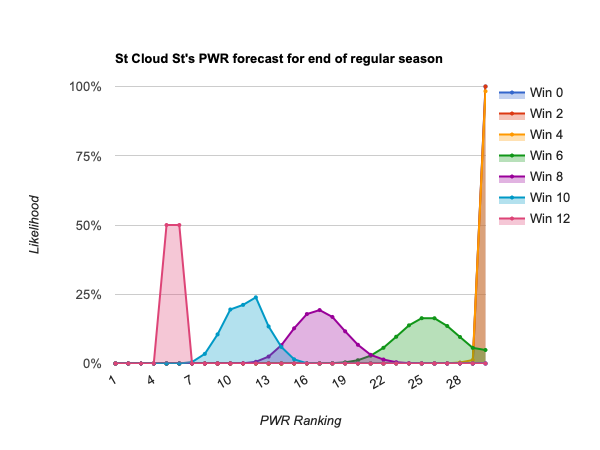
• #22 St Cloud St

• 

• 

#8 Massachusetts is nearly safe, only being able to dip as low as #11 if they have a season-ending loss on Thursday. But, their PWR could be negatively affected by the outcomes of remaining games in which they aren’t playing, and they wouldn’t quite be safe if they fell to #12-13 (those ranked teams would not get bids in the unlikely event that 4-5 conference autobids go to teams that wouldn’t otherwise make it at large).

While #9 Clarkson looks slightly safer, with minimal movement likely this weekend, they still have a best-of-3 conference tournament series remaining, which will carry the potential for downward movement.

The Hockey East and NCHC teams near the bottom of the list are alive because those conferences’ tournaments have not yet begun, so even with a winless weekend, those teams will have one more shot at raising their PWR with some wins.

Who can stay alive for an at-large bid only by winning this weekend?

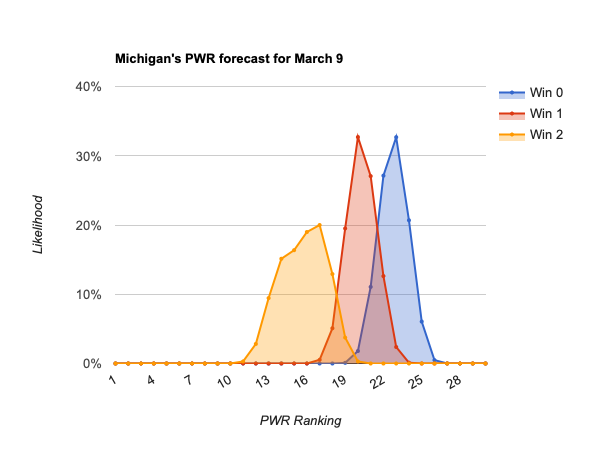
• #16 Michigan
• #17 Minnesota
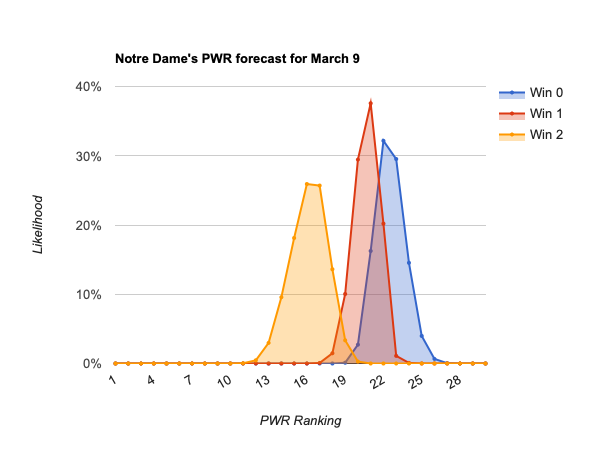
• #20 Notre Dame

The above listed teams will be below #16 in PWR if they lose this weekend, and eliminated form their conference tournament, so with no remaining shot at an NCAA bid.

• 

• 

• 

Whose only chance for an NCAA bid is winning their conference tournament?

• #23 Michigan State
• #24 Sacred Heart
• #25 Bowling Green
• #26 Northern Michigan
• #27 American International
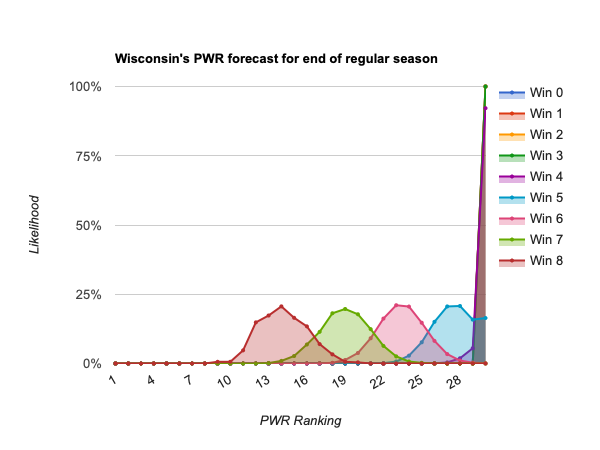
• #28 Wisconsin
• #29 Harvard
• #30 Boston University
• #31 New Hampshire
• #32 Connecticut
• #33 Alaska
• #34 Michigan Tech
• #35 Nebraska-Omaha
• #36 Rensselaer
• #37 RIT
• #38 Army
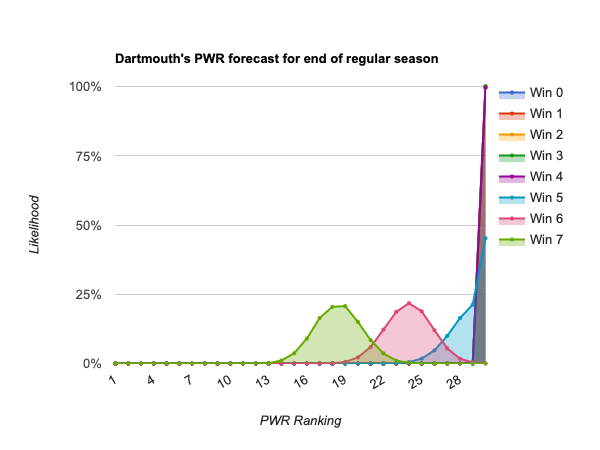
• #39 Dartmouth
• #40 Yale
• #41 Colorado College
• #42 Miami
• #43 Colgate
• #44 Lake Superior
• #45 Merrimack
• #46 Bentley
• #47 Niagara
• #48 Robert Morris
• #49 Air Force
• #50 Canisius
• #51 Holy Cross
• #52 Brown
• #53 Vermont
• #54 Union
• #55 Ferris St
• #56 Alaska Anchorage
• #57 Princeton
• #58 Alabama-Huntsville
• #59 St. Lawrence
• #60 Mercyhurst

What’s next?

The forecasts are updated weekly, usually Monday or Tuesday, so you can always browse them yourself. I’ll also try to post interesting interpretations here, with increasing frequency as we near the end of the regular season. Meanwhile, you can explore more of the data yourself:

• PWR Rankings
• PWR Forecast

How the forecast works

The forecast page notes when the forecast was last run (assume that it includes all games that had been completed as of that time).

Each forecast is based on at least one million monte carlo simulations of the games in the described period. For each simulation, the PairWise Ranking (PWR) is calculated and the results tallied. The probabilities presented in the forecasts are the share of simulations in which a particular outcome occurred.

The outcome of each game in each simulation is determined by random draw, with the probability of victory for each team set by their relative KRACH ratings. So, if the simulation set included a contest between team A with KRACH 300 and team B with KRACH 100, team A will win the game in very close to 75% of the simulations. I don’t simulate ties or home ice advantage.

Two weeks ago I identified 28 teams as still in the hunt for at-large bids. Of the 26 that are still in the hunt, 9 seem to have their at-large hopes on the line this weekend. For those teams, getting swept would seemingly knock them out of contention for an at-large bid.

As always, you might find it helpful to follow along in the end of season PWR forecast.

Who’s in the running, no matter what happens this weekend?

As mentioned weeks ago, the top 3 are essentially (though perhaps not mathematically) locks. Those are:
#1 North Dakota
#2 Minnesota St
#3 Cornell

For a big range of teams, a pair of wins this weekend would make their minimum likely end-of-season finish in the #11-13 range–not quite guaranteed a bid, but very likely. Those are:
#4 Minnesota-Duluth
#5 Denver
#6 Boston College
#7 Clarkson
#8 Massachusetts
#9 Penn St
#10 Arizona St
#11 Northeastern

Then, there just a couple teams that would still control their own destiny with a pair of losses this weekend. These teams could finish the regular season as high as #11-13 despite a pair of losses this weekend if they win the remainder of their games and get a bit lucky.

#12 Bemidji St
#13 Ohio St

Then, it gets interesting. The #14-28 block contains teams that would still be alive if swept interspersed with some that would seemingly be knocked out contention for an at-large bid if swept this weekend.

The teams that still seem to have a chance at an at-large bid, even if swept this weekend, are:
#15 Western Michigan
#16 Mass. Lowell
#17 Minnesota
#27 St Cloud St

Of those, only #15 Western Michigan could be deemed likely to have a shot at an at-large bid if they get swept this weekend but win out. The rest would be long shots after getting swept, even if they won out after that.

Who needs a win this weekend?

For most in that #14-28 range, however, getting swept this weekend would likely knock them out of contention for an at-large bid and put them in the position of needing a conference tournament win to make the NCAAs. Those teams are:

#14 Maine
#18 Quinnipiac
#19 Providence
#20 Michigan
#21 Boston University
#22 Notre Dame
#23 Michigan St
#26 Nebraska-Omaha
#28 New Hampshire

The first few of those can stay alive with a single win, while most need a pair of wins to stay in the hunt.

Whose only hope seem to be a conference tournament championship?

The rest of the teams don’t really stand much of a chance of an at-large bid anymore, no matter what happens. Those are:

#24 Northern Michigan
#25 Harvard
#29 American International
#30 Michigan Tech
#31 Bowling Green
#32 Sacred Heart
#33 Alaska
#34 RIT
#35 Army
#36 Wisconsin
#37 Dartmouth
#38 Yale
#39 Connecticut
#40 Rensselaer
#41 Colorado College
#42 Miami
#43 Colgate
#44 Lake Superior
#45 Holy Cross
#46 Bentley
#47 Merrimack
#48 Robert Morris
#49 Niagara
#50 Air Force
#51 Canisius
#52 Ferris St
#53 Union
#54 Brown
#55 Vermont
#56 Princeton
#57 Alaska Anchorage
#58 Alabama-Huntsville
#59 St. Lawrence
#60 Mercyhurst

Two weeks ago I wrote a First look at which teams are likely to make the 2020 NCAA hockey tournament. This article updates that with how the last two weekends’ results have changed the outlook.

Who’s a lock?

While two weeks ago there weren’t yet any mathematical guarantees, I no longer see any situation in which #1 North Dakota or #2 Minnesota State finish outside the top 10. Of course, I only search about 1,000,000 scenarios, so it might still be remotely possible (particularly if either lost out, which is so unlikely it’s still not showing up much in the scenarios).

Who’s in if they keep winning?

Two weeks ago, I identified #3 Cornell as a near lock, never dipping below #13 in the simulations. But, I did note that in the simulations Cornell never had fewer than 5 wins, so that a collapse which resulted in fewer than 5 wins in their final 12 games could push them out of contention. Cornell went 2-1-1 in the following weekends, leaving them still needing 3 more wins in their final 8 gams to be reasonably assured of being well situated going into the conference tournament.

Cornell’s situation hasn’t actually changed, Cornell is very likely to pick up the necessary wins with only two of its final eight opponents having winning records. But, as the number of games dwindles, noting how many they need to win is a bit more informative than declaring “they’re almost sure to make it”, as seemed reasonable in January.

#4 Denver is still in the position of needing to win about half of its remaining games to be sure, but will likely be in pretty good shape with just 2-3 more wins.

• 

• 

Who controls their own destiny?

As is to be expected this time of year, the list of teams that control their own destiny has gotten smaller. Only down through #30 St Cloud, are pretty much assured to be on the bubble if they win out.

Also, notably, #28 Michigan Tech can no longer climb onto the bubble, even if they win out.

The following teams can put themselves on the bubble if they perform well enough:
#5 Boston College
#6 Minnesota-Duluth
#7 Clarkson
#8 Massachusetts
#9 Northeastern
#10 Arizona St
#11 Ohio St
#12 Penn St
#13 Providence
#14 Quinnipiac
#15 Maine
#16 Northern Michigan
#17 Mass.-Lowell
#18 Minnesota
#19 Bemidji St
#20 Michigan St
#21 Western Michigan
#22 Notre Dame
#23 Harvard
#24 Boston University
#25 Nebraska-Omaha
#26 New Hampshire
#27 Sacred Heart
#29 Michigan
#30 St Cloud St

Of course, the teams near the top of that list require fewer wins than do teams at the bottom. Boston College will be in good shape with 5 wins, while St Cloud St really needs 8 to be sure.

• 

• 

Who needs help

Below that, only #31 Dartmouth and #35 Wisconsin show a significant chance of climbing onto the bubble if they win out. But they, like everyone else in this group, would likely need to win their conference tournament to prevent slipping back off the bubble with a season-ending loss.

The following teams should plan to win their conference tournaments if they want to make the NCAAs:
#28 Michigan Teach
#31 Dartmouth
#32 Alaska
#33 Army
#34 American International
#35 Wisconsin
#36 Bowling Gren
#37 RIT
#38 Connecticut
#39 Rensselaer
#40 Colgate
#41 Yale
#42 Colorado College
#43 Miami
#44 Holy Cross
#45 Bentley
#46 Air Force
#47 Robert Morris
#48 Lake Superior
#49 Merrimack
#50 Ferris St
#51 Canisius
#52 Union
#53 Niagara
#54 Princeton
#55 Vermont
#56 Alaska Anchorage
#57 Brown
#58 Alabama-Huntsville
#59 St. Lawrence
#60 Mercyhurst

• 

• 

What’s next?

The forecasts are updated weekly, usually Monday or Tuesday, so you can always browse them yourself. I’ll also try to post interesting interpretations here, with increasing frequency as we near the end of the regular season. Meanwhile, you can explore more of the data yourself:

• PWR Rankings
• PWR Forecast

How the forecast works

The forecast page notes when the forecast was last run (assume that it includes all games that had been completed as of that time).

Each forecast is based on at least one million monte carlo simulations of the games in the described period. For each simulation, the PairWise Ranking (PWR) is calculated and the results tallied. The probabilities presented in the forecasts are the share of simulations in which a particular outcome occurred.

The outcome of each game in each simulation is determined by random draw, with the probability of victory for each team set by their relative KRACH ratings. So, if the simulation set included a contest between team A with KRACH 300 and team B with KRACH 100, team A will win the game in very close to 75% of the simulations. I don’t simulate ties or home ice advantage.

Long time followers of PWR know that despite seeming pretty stable overall, individual teams’ PWR rankings can move substantially under the right conditions. An 8-10 position swing in a single weekend’s pair of games is a relatively common possibility, though it often takes both an unusual outcome for the team and a lot of other things going just right around the league.

This week, however, the #31 Maine Black Bears face a stunning 18 position upside potential in their series against #5 Boston College. While the full 18 position climb is exceedingly unlikely, occurring in only 1.1% of scenarios in which Maine sweeps BC, Maine’s likely PWR ranking if they sweep are centered around #16, a 15 spot climb!

Digging into why such a big move is possible for Maine, there’s nothing unique about their situation, there are just lots of known little things about PWR and RPI adding up just right for the Black Bears facing a series they’re supposed to lose.

Warning, thar be math below!

At 10-9-4, Maine has a win percentage of .5217, and winning two more would move that to 12-9-4 and .5600. But, because of RPI game weightings (in which road wins and home losses count more than road losses and home wins), Maine’s current weighted percentage is actually .5490 and would rise to .5965 with a pair of road wins this weekend. Maine is undefeated at home, but home wins only count as 4/5 of a game, as do road losses. But, road wins would count as 6/5 of a game, giving them 50% more impact on Maine’s ratings, giving these games (if wins) outsized influence on Maine’s ratings. The other components of Maine’s RPI would also rise a bit because of BC’s strong schedule, though much more modestly (oppponents’ win% from .4927 to .5197, and opponents’ opponents’ win% from .4958 to .5012). Finally, Maine’s quality win bonus would climb from .0019 to .0057 with a pair of road wins against Boston College.

Adding all of that up, Maine’s RPI would climb from .5103 to about .5346 with a pair of road wins this weekend.

Maine’s position near the bottom of a dense cluster of RPI rankings would result in an RPI climb of .0243 leading to a substantial climb in PWR ranking. Looking at the current RPI rankings, an RPI of .5346 would be good for #16 today, 15 spots higher than Maine’s current ranking. For comparison, if Maine were .0243 lower, at .4860 RPI, they would still be #40, only 9 positions lower.

Is this really going to happen?

Of course, a road sweep against #5 Boston College (15-5-0) is a tall order. Assuming no home ice advantage, KRACH predicts Maine as only having a 19% chance of winning each game, or a 3.7% chance of the sweep (if the games were independent). But, if Maine pulled off this signature sweep, RPI and PWR would statistically reward the Black Bears for being a different team than their results to date would predict.

With 10-12 regular season games remaining for most teams, we can start to get some picture of what teams need to do to end the regular season in position for an NCAA tournament bid (we generally think of ending the regular season in the top 10 as likely being in the tournament, anywhere from 10-15 as on the bubble, and 16 or below as unlikely to make it at-large).

If you’re new to this site or missed last week’s article, First PWR Forecast of 2020 (and why you might care), read that first for some background.

You can always browse the weekly forecast yourself, and might find it useful to follow along with this article, at PWR by wins forecast.

Who’s a lock?

This far out, there are no mathematical locks. Even #1 North Dakota could miss if the Hawks improbably strung together 12 losses to end their regular season. But, in 1,000,000 simulations, none of #1 North Dakota, #2 Minnesota State, or #3 Cornell dipped below #13 (with 2, 4, and 5 being the minimum number of wins simulated for each, respectively). It would take an unprecedented collapse for any of the three to miss.

• 

• 

• 

Unless something fundamentally changes that makes their success to date not predictive of future results, it would take a 1 in a 1,000,000 collapse for any of the following teams to miss the NCAA tournament:
#1 North Dakota
#2 Minnesota State
#3 Cornell

Who’s in if they keep performing as they have to date?

Surprisingly, in addition to the above, only #4 Denver seems almost assured an at-large berth if they win half their remaining games.

• 

The lone team likely to be assured a berth if they keep winning is:
#4 Denver

Who controls their own destiny?

From #5 Boston College down to about #34 St Cloud State can put themselves in bubble position or better with sufficiently good performance over the remainder of the regular season.

Those teams include:
#5 Boston College
#6 Massachusetts
#7 Ohio State
#8 Clarkson
#9 Penn State
#10 Providence
#11 Arizona State
#12 Minnesota-Duluth
#13 Mass.-Lowell
#14 Northeastern
#15 Quinnipiac
#16 Michigan State
#17 Northern Michigan
#18 New Hampshire
#19 Dartmouth
#20 Harvard
#21 Notre Dame
#22 Michigan Tech
#23 Bemidji State
#24 Michigan
#25 Army
#26 Western Michigan
#27 Bowling Green
#28 Nebraska-Omaha
#29 Alaska
#30 Boston University
#31 Maine
#32 Wisconsin
#33 Minnesota
#34 St. Cloud St

Of course, teams near the top of that list have an easier path (winning about 50% of remaining games for #5 Boston College) than teams near the bottom of that list (winning about 80% of remaining games for #34 St. Cloud St).

• 

• 

Who needs help

From #35 down, there aren’t a lot of opportunities to climb onto the bubble. Quite a few in the #35-45 range seem to have a possibility of climbing just onto the bubble with a perfect or near perfect remainder of the regular season. But, even if that unlikely outcome were to occur, anything short of a conference tournament championship would result in a season ending loss that would likely push them back out of contention for an at-large bid. If you like super long shots, the teams with the best chance of that scenario are #35 Sacred Heart, #36 Connecticut, #37 Colorado College, #39 Colgate, and #41 Yale.

The following teams should plan to win their conference tournaments if they want to make the NCAAs:
#35 Sacred Heart
#36 Connecticut
#37 Colorado College
#38 American International
#39 Colgate
#40 RIT
#41 Yale
#42 Miami
#43 Rensselaer
#44 Air Force
#45 Robert Morris
#46 Holy Cross
#47 Lake Superior
#48 Merrimack
#49 Canisius
#50 Bentley
#51 Vermont
#52 Ferris State
#53 Princeton
#54 Union
#55 Niagara
#56 Alaska Anchorage
#57 Brown
#58 Mercyhurst
#59 St. Lawrence
#60 Alabama-Huntsville

What next?

The forecasts are updated weekly, usually Monday or Tuesday, so you can always browse them yourself. I’ll also try to post interesting interpretations here, with increasing frequency as we near the end of the regular season. Meanwhile, you can explore more of the data yourself:

• PWR Rankings
• PWR Forecast

This post explains the data in the PWR tournament possibilities page. You can follow along there if you’d like to browse the raw data yourself:

NCAA Tournament Participation Probabilities

Who’s in?

The following 10 teams are guaranteed an invitation to the NCAA tournament on the basis of their PWR.

• #1 St Cloud State
• #2 Massachusetts
• #3 Minnesota St
• #4 Minnesota-Duluth
• #5 Quinnipiac
• #6 Denver
• #7 Ohio State
• #8 Northeastern
• #9 Clarkson
• #10 Arizona St

Who else can get in?

The winner of each conference tournament can get in:

Atlantic Hockey

• American International (*)
• Robert Morris (*)
• Niagara (*)
• RIT (*)

Big Ten

• Notre Dame (*)
• Penn St (*)

Hockey East

• Massachusetts (in)
• Boston College (*)
• Boston University (*)
• Northeastern (in)

ECAC

• Cornell
• Brown (*)
• Harvard
• Clarkson (in)

NCHC

• St Cloud St (in)
• Colorado College (*)
• Denver (in)
• Minnesota Duluth (in)

WCHA

• Minnesota St (in)
• Bowling Green

Those marked with a (*) can only get in if they win their conference tournament. Those marked with (in) will make the tournament regardless of conference outcome. But, what about the rest?

There are 16 spots in the NCAA tournament. 10 participants are already known (see above). The winners of the Atlantic Hockey and Big Ten tournaments are not only guaranteed spots, but are the only teams from those conference tournaments that will get spots, so you can think of those two spots as reserved for one of the 4 AH teams and one of the 2 AH teams, respectively.

That leaves 4 spots total for a combination of the champions of the remaining 4 conferences and the 5 teams that can make it at-large (there is some overlap between those two groups). How many teams are selected at-large depends how many of the 4 remaining slots are taken by teams that aren’t already in by virtue of their PWR. For each of Hockey East, ECAC, NCHC, and WCHA that are won by a team that is already counted as being in, an additional spot is available for a different team to make it at-large.

The following teams can make it at-large:

• Cornell (64% of scenarios in which they win 0, 97% in which they win 1)
• Harvard (81% of scenarios in which they win 0, 94% in which they win 1)
• Bowling Green (29% of scenarios in which they lose)
• Providence (not playing, 65% of scenarios)
• Union (not playing, <.1% of scenarios)

With some conference tournaments beginning this weekend, the NCAA tournament outlook for most teams is pretty well known. But, a few teams in the middle are jockeying for bubble position, hoping to get an at-large bid should their conference tournament runs fall short. This article looks at what is likely to happen in the PWR rankings this weekend.

I’ll pull out the highlights, but you can follow along in the table that shows the likely outcomes for all teams:

Wins needed to likely have PWR rank on March 11, 2019

#1 St Cloud is almost certain to still be #1 next Monday, no matter what happens this weekend.

#2 Massachusetts through #7 Ohio State should still be the same set of teams, but perhaps reshuffled based on outcomes (even the teams not playing, #5 Quinnipiac and #7 Ohio State, could move a bit).

Those teams include:
#2 Massachusetts
#3 Minnesota-Duluth
#4 Minnesota St
#5 Quinnipiac
#6 Denver
#7 Ohio State

#8-#20 are fighting for bubble position and (where applicable) hoping to move on for additional opportunities to improve their PWR and at-large bid likelihood.

Those teams include:
#8 Arizona St
#9 Providence
#10 Clarkson
#11 Northeastern
#12 Cornell
#13 Harvard
#14 Western Michigan
#15 Notre Dame
#16 Penn St
#17 Bowling Green
#18 Mass.-Lowell
#19 Union
#20 North Dakota

#21 Minnesota and below are almost certain to remain outside the top 16, regardless of this weekend’s outcome, so facing long shots to make the NCAA tournament at large.